top of page

Key Concept
-
Arc Length and Sector Area
-
Area of Triangle
-
Application of Trigonometry: Elevation Angles and Depression Angles
Instructional Videos
Angles of elevation and depression
The term angle of elevation denotes the angle from the horizontal upward to an object. An observer's line of sight would be above the horizontal.
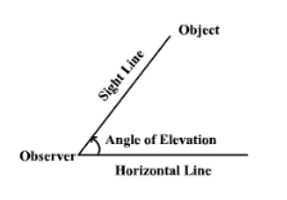
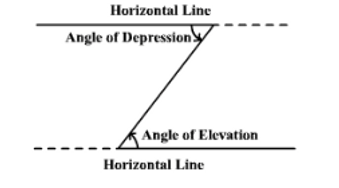
The term angle of depression denotes the angle from the horizontal downward to an object. An observer's line of sight would be below the horizontal.
Note that the angle of elevation and the angle of depression are congruent.

Examples of Work
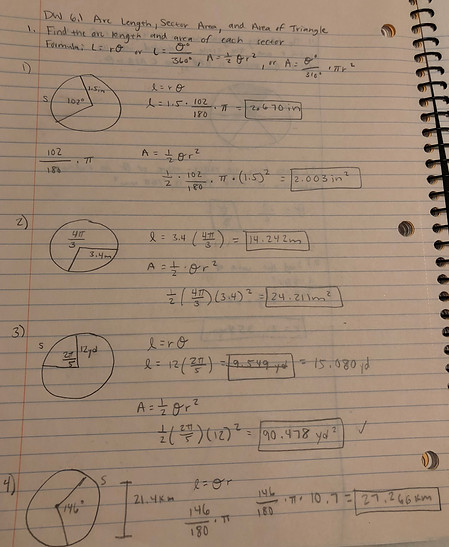
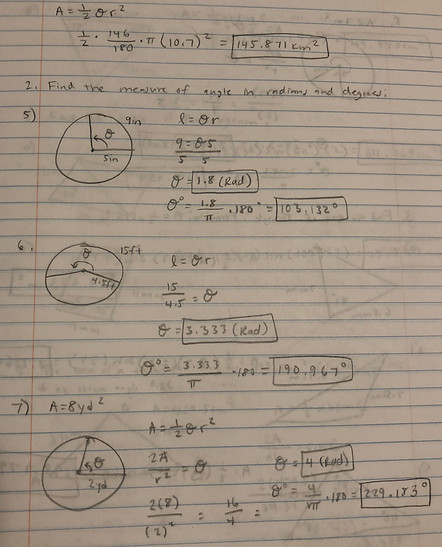


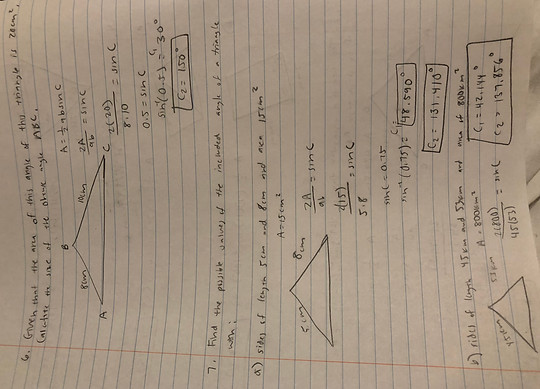

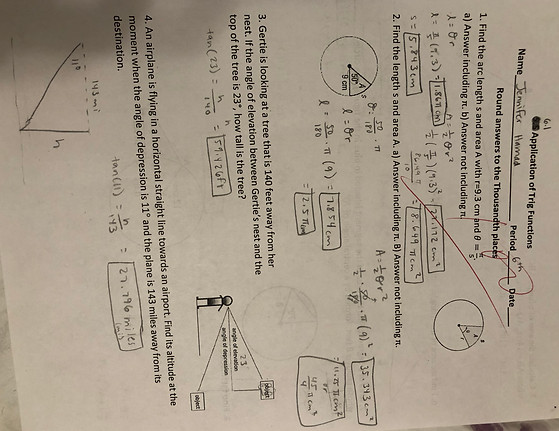
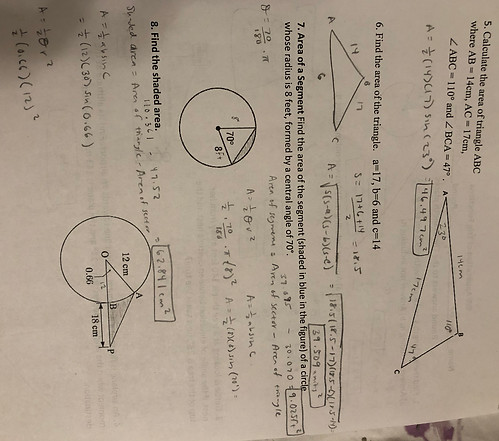
Lesson Summary: By the end of this lesson, students should be able to utilize the equation l=Or to solve for arc length as well as manipulate the equation to solve for the other two variables (the radius and central angle in radians). To illustrate students should be able to utilize the equation A= 1/2Or^2 to solve for the area of a sector as well as be able to use the equation to solve for the other two variables of radius and central angle in radians. For triangles, students should be able to use the equation A=1/2absinC to solve for the area of a triangle as well as manipulate the equation to solve for the two possible included angles (obtuse and acute) or solve for the missing side of a or b. Lastly, students should understand how to use SohCahToa to solve for various real world application problems affiliated with angles of elevation and depression.
bottom of page